Convex sets

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Generate a convex polygon (e.g., a convex hull of some points)
points = np.array([
    [1, 1], [2, 3], [4, 4], [6, 3], [5, 1], [3, 0]
])

# Choose two points inside the polygon
A = np.array([2.5, 2])
B = np.array([4.5, 2.5])

# Line segment between A and B
t = np.linspace(0, 1, 100)
segment = np.outer(1 - t, A) + np.outer(t, B)

# Plot the convex set and the line segment
plt.figure(figsize=(8, 6))
plt.fill(points[:, 0], points[:, 1], alpha=0.3, label="Convex Set", edgecolor='blue')
plt.plot(segment[:, 0], segment[:, 1], 'r--', label="Line segment AB")
plt.plot(*A, 'ro', label="Point A")
plt.plot(*B, 'go', label="Point B")

plt.title("A Convex Set")
plt.xlabel("x")
plt.ylabel("y")
plt.axis("equal")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

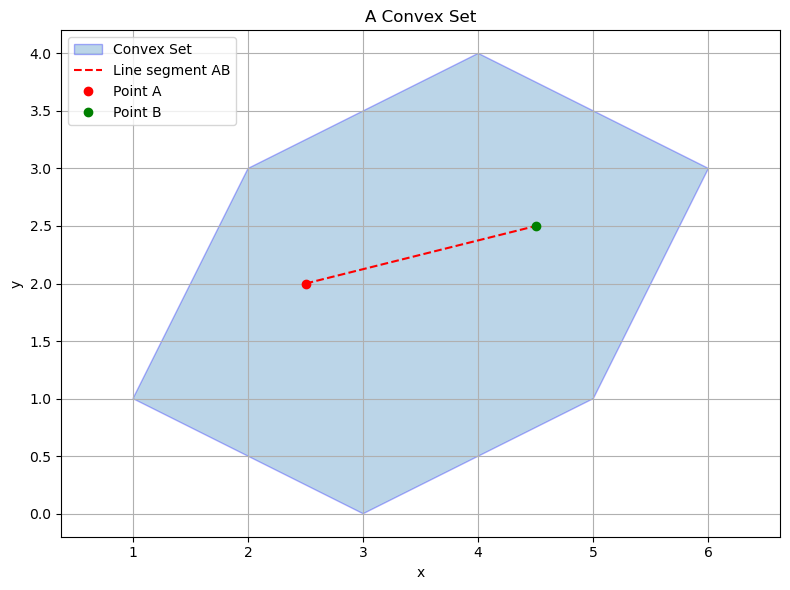
This figure visualizes a convex set: a polygon where the line segment connecting any two points within the set (e.g., points A and B) lies entirely inside the set. The red dashed line confirms this key geometric property of convex sets.

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np

# Define a non-convex polygon (e.g., a simple star shape or concave polygon)
points = np.array([
    [1, 1], [2, 3], [3, 1.5], [4, 3], [5, 1], [3, 0]
])

# Choose two points inside the set where the connecting line goes outside
A = np.array([2, 2])
B = np.array([4, 2])

# Line segment between A and B
t = np.linspace(0, 1, 100)
segment = np.outer(1 - t, A) + np.outer(t, B)

# Plot the non-convex set and the line segment
plt.figure(figsize=(8, 6))
plt.fill(points[:, 0], points[:, 1], alpha=0.3, label="Non-Convex Set", edgecolor='blue')
plt.plot(segment[:, 0], segment[:, 1], 'r--', label="Line segment AB")
plt.plot(*A, 'ro', label="Point A")
plt.plot(*B, 'go', label="Point B")

plt.title("A Non-Convex Set")
plt.xlabel("x")
plt.ylabel("y")
plt.axis("equal")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

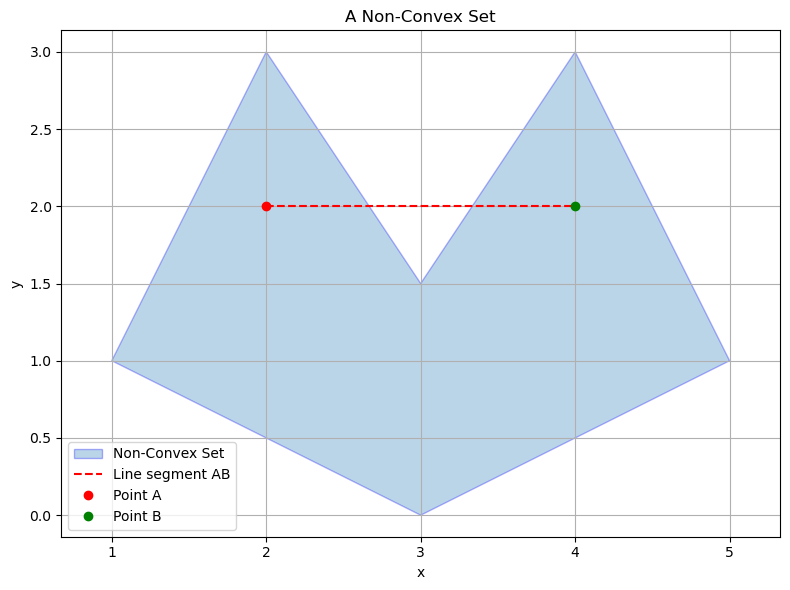
This figure illustrates a non-convex set: a shape where the line segment between two points inside the set (A and B) partially lies outside the set. This violation of the convexity condition distinguishes non-convex sets from convex ones.

A set \(\mathcal{X} \subseteq \mathbb{R}^d\) is convex if

\[t\mathbf{x} + (1-t)\mathbf{y} \in \mathcal{X}\]

for all \(\mathbf{x}, \mathbf{y} \in \mathcal{X}\) and all \(t \in [0,1]\).

Geometrically, this means that all the points on the line segment between any two points in \(\mathcal{X}\) are also in \(\mathcal{X}\).

Why do we care whether or not a set is convex? We will see later that the nature of minima can depend greatly on whether or not the feasible set is convex. Undesirable pathological results can occur when we allow the feasible set to be arbitrary, so for proofs we will need to assume that it is convex.

Fortunately, we often want to minimize over all of \(\mathbb{R}^d\), which is easily seen to be a convex set.