The Gaussian distribution

The Gaussian distribution#

There are many distributions, but one of particular importance is the Gaussian distribution, also known as the normal distribution.

It is a continuous distribution, parameterized by its mean \(\boldsymbol\mu \in \mathbb{R}^d\) and positive-definite covariance matrix \(\mathbf{\Sigma} \in \mathbb{R}^{d \times d}\), with density

\[p(\mathbf{x}; \boldsymbol\mu, \mathbf{\Sigma}) = \frac{1}{\sqrt{(2\pi)^d \det(\mathbf{\Sigma})}}\exp\left(-\frac{1}{2}(\mathbf{x} - \boldsymbol\mu)^{\!\top\!}\mathbf{\Sigma}^{-1}(\mathbf{x} - \boldsymbol\mu)\right)\]

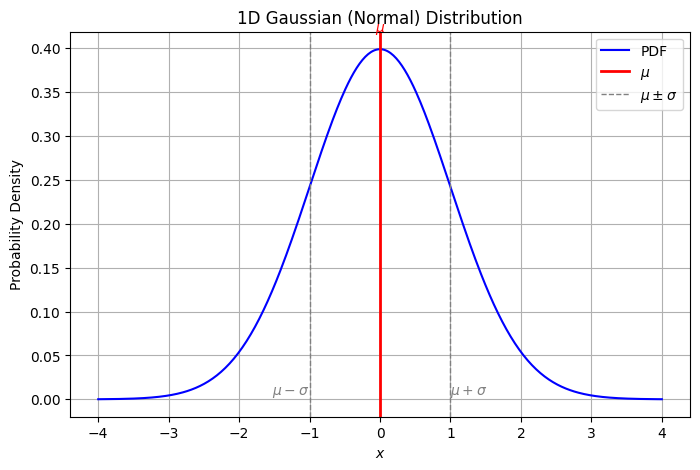
Note that in the special case \(d = 1\), the density is written in the more recognizable form

\[p(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\]

../_images/72cb702d99603188a5bfdd59154d4bf53a12249522328f1a97e5cce1976403aa.png

We write \(\mathbf{X} \sim \mathcal{N}(\boldsymbol\mu, \mathbf{\Sigma})\) to denote that \(\mathbf{X}\) is normally distributed with mean \(\boldsymbol\mu\) and variance \(\mathbf{\Sigma}\).

The geometry of multivariate Gaussians#

The geometry of the multivariate Gaussian density is intimately related to the geometry of positive definite quadratic forms.

First observe that the p.d.f. of the multivariate Gaussian can be rewritten as a normalized exponential function of a quadratic form:

\[p(\mathbf{x}; \boldsymbol\mu, \mathbf{\Sigma}) = \underbrace{\frac{1}{\sqrt{(2\pi)^d \det(\mathbf{\Sigma})}}}_{\text{normalization constant}} \exp\left(-\frac{1}{2} {\left(\mathbf{x}-\boldsymbol\mu\right)}^{\!\top\!}\mathbf{\Sigma}^{-1}{\left(\mathbf{x}-\boldsymbol\mu\right)}\right)\]

The multiplicative term \(\frac{1}{\sqrt{(2\pi)^d \det(\mathbf{\Sigma})}}\) is a normalization constant that is independent of \(\mathbf{x}\) and ensures that the density integrates to 1.

The random variable \(\mathbf{x}\) is present only in the exponent. Thus, the multiplicative term \(\frac{1}{\sqrt{(2\pi)^d \det(\mathbf{\Sigma})}}\) is a constant that ensures that the Gaussian probability density function integrates to 1.

To gain a better understanding of the geometry of the Gaussian density, we can leave out the normalization constant and focus on the exponential function of the quadratic form:

\[p(\mathbf{x}; \boldsymbol\mu, \mathbf{\Sigma}) \propto \exp\left(-\frac{1}{2} {\left(\mathbf{x}-\boldsymbol\mu\right)}^{\!\top\!}\mathbf{\Sigma}^{-1}{\left(\mathbf{x}-\boldsymbol\mu\right)}\right)\]

Expanding the quadratic form, we get:

\[\begin{split} \begin{aligned} p(\mathbf{x}; \boldsymbol\mu, \mathbf{\Sigma}) &\propto \exp\left(-\frac{1}{2} {\left(\mathbf{x}^{\!\top\!}\mathbf{\Sigma}^{-1}\mathbf{x} - 2\mathbf{x}^{\!\top\!}\mathbf{\Sigma}^{-1}\boldsymbol\mu + \boldsymbol\mu^{\!\top\!}\mathbf{\Sigma}^{-1}\boldsymbol\mu\right)}\right) \\ &= \exp\left(-\frac{1}{2} {\left(\mathbf{x}^{\!\top\!}\mathbf{\Sigma}^{-1}\mathbf{x} - 2\mathbf{x}^{\!\top\!}\mathbf{\Sigma}^{-1}\boldsymbol\mu + \boldsymbol\mu^{\!\top\!}\mathbf{\Sigma}^{-1}\boldsymbol\mu\right)}\right)\\ &= \exp\left(-\frac{1}{2} {\left(\mathbf{x}^{\!\top\!}\mathbf{\Sigma}^{-1}\mathbf{x} - 2\mathbf{x}^{\!\top\!}\mathbf{\Sigma}^{-1}\boldsymbol\mu \right)}\right)\underbrace{\exp\left(-\frac{1}{2} {\boldsymbol\mu^{\!\top\!}\mathbf{\Sigma}^{-1}\boldsymbol\mu}\right)}_{\text{constant}} \end{aligned} \end{split}\]

We identify another multiplicative term that does not depend on \(\mathbf{x}\) and can be moved into the normalization constant.

So, if we only look at the part that depends on \(\mathbf{x}\), what are are left with is:

\[ p(\mathbf{x}; \boldsymbol\mu, \mathbf{\Sigma}) \propto \exp\left(-\frac{1}{2} {\mathbf{x}^{\!\top\!}\mathbf{\Sigma}^{-1}\mathbf{x}} + \boldsymbol\mu^{\!\top\!}\mathbf{\Sigma}^{-1}\mathbf{x} \right) \]

Here is a key observation: the function \(\exp(-z)\) is strictly monotonically decreasing in its argument \(z\in\mathbb{R}\). That is, \(\exp(-a) > \exp(-b)\) whenever \(a < b\).

This means that the probability density is highest at the mean \(\boldsymbol\mu\) and falls off exponentially with the distance from the mean.

Furthermore, because \(\exp(-z)\) is strictly monotonic, it is injective, so the \(c\)-isocontours of \(p(\mathbf{x}; \boldsymbol\mu, \mathbf{\Sigma})\) are the \(\exp(-z)^{-1}(c)\)-isocontours of the quadratic form \(\mathbf{x} \mapsto \frac{1}{2}\mathbf{x}^{\!\top\!}\mathbf{\Sigma}^{-1}\mathbf{x} + \boldsymbol\mu^{\!\top\!}\mathbf{\Sigma}^{-1}\mathbf{x}\).

Recall that the isocontours of a quadratic form associated with a positive definite matrix \(\mathbf{A}\) are ellipsoids such that the axes point in the directions of the eigenvectors of \(\mathbf{A}\), and the lengths of these axes are proportional to the inverse square roots of the corresponding eigenvalues.

Therefore in this case, the isocontours of the density are ellipsoids (centered at \(\boldsymbol\mu\)) with axis lengths proportional to the inverse square roots of the eigenvalues of the so-called precision matrix \(\mathbf{\Sigma}^{-1}\), or equivalently, the square roots of the eigenvalues of \(\mathbf{\Sigma}\).

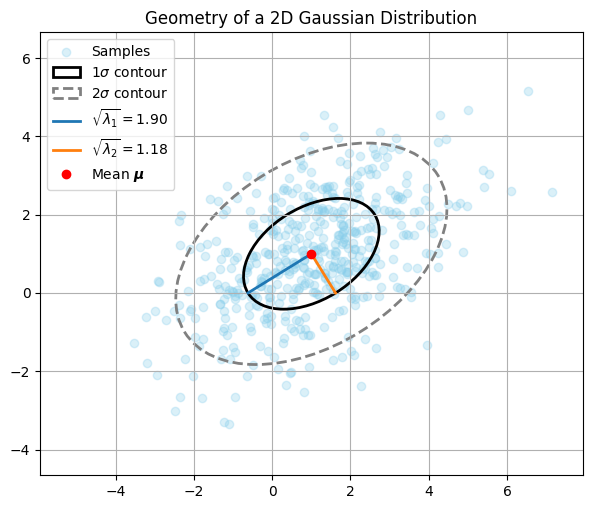
../_images/62dbc6bd2743bae616e3be6fa16e407a3e1f64a03f92e8eed11f3e191c971978.png

In the plot, the solid elipse shows the \(1\sigma\) contour of the Gaussian density.

Within the ellipse, roughly half the samples are located.
The orientation of the ellipse is given by the eigenvectors of \(\Sigma\), shown as blue and orange lines.
The axis lengths are proportional to the square roots of the eigenvalues of \(\Sigma\) (or inverse square roots of \(\Sigma^{-1}\)).

The dashed ellipse shows the \(2\sigma\) contour containing roughly 95% of the samples.

Completing the square#

Let’s dig a bit deeper into the observation that the Gaussian density is proportional to a \(\exp(-z)\), where \(z\) is a quadratic form associated with the positive definite precision matrix \(\mathbf{\Sigma}^{-1}\).

\[ p(\mathbf{x}) = \underbrace{\frac{\exp\left(-\frac{1}{2} \boldsymbol\mu^{\!\top\!}\mathbf{\Sigma}^{-1}\boldsymbol\mu\right)}{\sqrt{(2\pi)^d \det(\mathbf{\Sigma})}}}_{\text{constant}}\cdot \exp\left(-\frac{1}{2} {\mathbf{x}^{\!\top\!}\mathbf{\Sigma}^{-1}\mathbf{x}} + \boldsymbol\mu^{\!\top\!}\mathbf{\Sigma}^{-1}\mathbf{x} \right) \]

A key observation is that all terms in the Gaussian density that depend on \(\mathbf{x}\) appear in the quadratic form and that the remaining constant term merely ensures that the density integrates to 1.

\[ \begin{aligned} \int \exp\left(-\frac{1}{2} {\mathbf{x}^{\!\top\!}\mathbf{\Sigma}^{-1}\mathbf{x}} + \boldsymbol\mu^{\!\top\!}\mathbf{\Sigma}^{-1}\mathbf{x} \right) d\mathbf{x}= \frac{\sqrt{(2\pi)^d \det(\mathbf{\Sigma})}}{\exp\left(-\frac{1}{2} \boldsymbol\mu^{\!\top\!}\mathbf{\Sigma}^{-1}\boldsymbol\mu\right)} \end{aligned} \]

This obervation is sufficient to conclude that any distribution that is proportional to \(\exp(-z)\), where \(z\) is a quadratic form associated with a positive definite matrix \(\mathbf{A}\), is a Gaussian distribution.

Further, we can use this observation to derive the mean \(\boldsymbol\mu\) and covariance \(\mathbf{\Sigma}\) of this Gaussian distribution. As the Gaussian distribution is fully determined by its mean and covariance, this is sufficient to fully specify the distribution.

Let’s formalize this observation in a theorem.

Theorem (Completing the Gaussian square)

Let \(p(\mathbf{x}) \propto \exp(-z(\mathbf{x}))\) be a distribution that is proportional to a \(\exp(-z)\), where \(z\) is a quadratic form associated with a positive definite matrix \(\mathbf{A}\).

\[ p(\mathbf{x}) \propto \exp\left( -\frac{1}{2} \mathbf{x}^\top \mathbf{A} \mathbf{x} + \mathbf{b}^\top \mathbf{x} \right) \]

Then the distribution is a Gaussian distribution with mean \(\boldsymbol\mu\) and covariance \(\mathbf{\Sigma}\) given by

\[ \boldsymbol\mu = \mathbf{A}^{-1} \mathbf{b} \quad \text{and} \quad \mathbf{\Sigma} = \mathbf{A}^{-1} \]

To see that the expressions for the mean and covariance are correct, we expand the desired square:

\[ -\frac{1}{2} (\mathbf{x} - \boldsymbol\mu)^\top \mathbf{A} (\mathbf{x} - \boldsymbol\mu) = -\frac{1}{2} \mathbf{x}^\top \mathbf{A} \mathbf{x} + \mathbf{b}^\top \mathbf{x} + \text{const} \]

Let’s expand the LHS:

\[ -\frac{1}{2} \left[ \mathbf{x}^\top \mathbf{A} \mathbf{x} - 2 \boldsymbol\mu^\top \mathbf{A} \mathbf{x} + \boldsymbol\mu^\top \mathbf{A} \boldsymbol\mu \right] = -\frac{1}{2} \mathbf{x}^\top \mathbf{A} \mathbf{x} + \boldsymbol\mu^\top \mathbf{A} \mathbf{x} + \text{const} \]

So we want:

\[ \boldsymbol\mu^\top \mathbf{A} \mathbf{x} = \mathbf{b}^\top \mathbf{x} \quad \Rightarrow \quad \boldsymbol\mu^\top \mathbf{A} = \mathbf{b}^\top \quad \Rightarrow \quad \mathbf{A} \boldsymbol\mu = \mathbf{b} \quad \Rightarrow \quad \boldsymbol\mu = \mathbf{A}^{-1} \mathbf{b} \]

Hence,

\[ p(\mathbf{x}) \propto \exp\left( -\frac{1}{2} (\mathbf{x} - \mathbf{A}^{-1} \mathbf{b})^\top \mathbf{A} (\mathbf{x} - \mathbf{A}^{-1} \mathbf{b}) \right) \]

or equivalently,

\[ p(\mathbf{x}) = \mathcal{N}(\mathbf{x}; \mathbf{A}^{-1} \mathbf{b}, \mathbf{A}^{-1}) \]

This technique is called completing the square and is a standard technique when working with normal distributions.

To put it into practice, we will now use it to derive the marginal and conditional distributions of a Gaussian distribution.

Conditional Gaussian distributions#

Let \(\mathbf{x} \sim \mathcal{N}(\boldsymbol\mu, \mathbf{\Sigma})\) be the joint distribution of two random variables \(\mathbf{x}_1\) and \(\mathbf{x}_2\), where

\[\begin{split} \mathbf{x} = \begin{bmatrix} \mathbf{x}_1 \\ \mathbf{x}_2 \end{bmatrix}, \quad \boldsymbol\mu = \begin{bmatrix} \boldsymbol\mu_1 \\ \boldsymbol\mu_2 \end{bmatrix}, \quad \mathbf{\Sigma} = \begin{bmatrix} \mathbf{\Sigma_{11}} & \mathbf{\Sigma_{12}} \\ \mathbf{\Sigma_{21}} & \mathbf{\Sigma_{22}} \end{bmatrix} \end{split}\]

Let \(\mathbf{\Lambda}=\mathbf{\Sigma}^{-1}\) be the joint precision matrix.

We can partition the joint precision matrix as follows:

\[\begin{split} \mathbf{\Lambda} = \begin{bmatrix} \mathbf{\Lambda_{11}} & \mathbf{\Lambda_{12}} \\ \mathbf{\Lambda_{21}} & \mathbf{\Lambda_{22}} \end{bmatrix} \end{split}\]

We know that the conditional distribution of \(\mathbf{x}_1 \mid \mathbf{x}_2\) is given by the joint distribution divided by the marginal distribution of \(\mathbf{x}_2\):

\[ p(\mathbf{x}_1 \mid \mathbf{x}_2) = \frac{p(\mathbf{x}_1, \mathbf{x}_2)}{p(\mathbf{x}_2)} \]

As the marginal distribution of \(\mathbf{x}_2\) does not depend on \(\mathbf{x}_1\) it can be seen as a constant.

Thus, the conditional distribution of \(\mathbf{x}_1 \mid \mathbf{x}_2\) is proportional to their joint distribution.

In order to find the conditional distribution, we need to find all terms that depend on \(\mathbf{x}_1\) and complete the square.

\[\begin{split} \begin{aligned} p(\mathbf{x}_1 \mid \mathbf{x}_2) &\propto p(\mathbf{x}_1, \mathbf{x}_2)\\ &\propto \exp\left( -\frac{1}{2}(\mathbf{x}_1-\mathbf{\mu}_1)^\top \mathbf{\Lambda_{11}} (\mathbf{x}_1-\mathbf{\mu}_1) -\frac{1}{2} (\mathbf{x}_2-\mathbf{\mu}_2)^\top \mathbf{\Lambda_{22}} (\mathbf{x}_2-\mathbf{\mu}_2) - (\mathbf{x}_1-\mathbf{\mu}_1)^\top \mathbf{\Lambda_{12}} (\mathbf{x}_2-\mathbf{\mu}_2) \right) \\ &\propto \exp\left( -\frac{1}{2}(\mathbf{x}_1-\mathbf{\mu}_1)^\top \mathbf{\Lambda_{11}} (\mathbf{x}_1-\mathbf{\mu}_1) - (\mathbf{x}_2-\mathbf{\mu}_2)\mathbf{\Lambda_{21}} (\mathbf{x}_1-\mathbf{\mu}_1)^\top\right) \\ &\propto \exp\left( -\frac{1}{2}\mathbf{x}_1^\top \mathbf{\Lambda_{11}} \mathbf{x}_1 + \mathbf{\mu}_1^\top\mathbf{\Lambda_{11}} \mathbf{x}_1 + (\mathbf{x}_2 - \mathbf{\mu}_2)^\top \mathbf{\Lambda_{21}}\mathbf{x}_1 \right) \\ &= \exp\left( -\frac{1}{2}\mathbf{x}_1^\top \mathbf{\Lambda_{11}} \mathbf{x}_1 + \left(\mathbf{\Lambda_{11}}\mathbf{\mu}_1 +\mathbf{\Lambda_{12}} (\mathbf{x}_2 - \mathbf{\mu}_2) \right)^\top\mathbf{x}_1\right) \end{aligned} \end{split}\]

It follows that we can identify the squared form in \(\mathbf{x}_1\) associated with the postive definite matrix \(\mathbf{A}\) and the vector \(\mathbf{b}\) equal to

\[ \mathbf{A}=\mathbf{\Lambda_{11}} \quad \text{and} \quad \mathbf{b}=\left(\mathbf{\Lambda_{11}}\mathbf{\mu}_1 +\mathbf{\Lambda_{12}} (\mathbf{x}_2 - \mathbf{\mu}_2) \right) \]

Thus, the conditional distribution is a Gaussian with mean and covariance matrix given by

\[ p(\mathbf{x}_1 \mid \mathbf{x}_2) = \mathcal{N}(\mathbf{x}_1; \mu_{1\mid2}, \Sigma_{1\mid2}) \]

\[ \Sigma_{1\mid2} = \mathbf{\Lambda_{11}}^{-1} \]

and mean

\[\begin{split} \begin{aligned} \mu_{1\mid2} &= \mathbf{\Lambda_{11}}^{-1}\left(\mathbf{\Lambda_{11}}\mathbf{\mu}_1 +\mathbf{\Lambda_{12}} (\mathbf{x}_2 - \mathbf{\mu}_2) \right) \\ &= \mathbf{\mu}_1 + \mathbf{\Lambda_{11}}^{-1}\mathbf{\Lambda_{12}} (\mathbf{x}_2 - \mathbf{\mu}_2) \end{aligned} \end{split}\]

Using the blockwise matrix inversion theorem (TODO appendix), these can alternatively been written as

\[ \mu_{1\mid2} = \mu_1 + \Sigma_{12} \Sigma_{22}^{-1}(x_2 - \mu_2), \quad \Sigma_{1\mid2} = \Sigma_{11} - \Sigma_{12} \Sigma_{22}^{-1} \Sigma_{21} \]

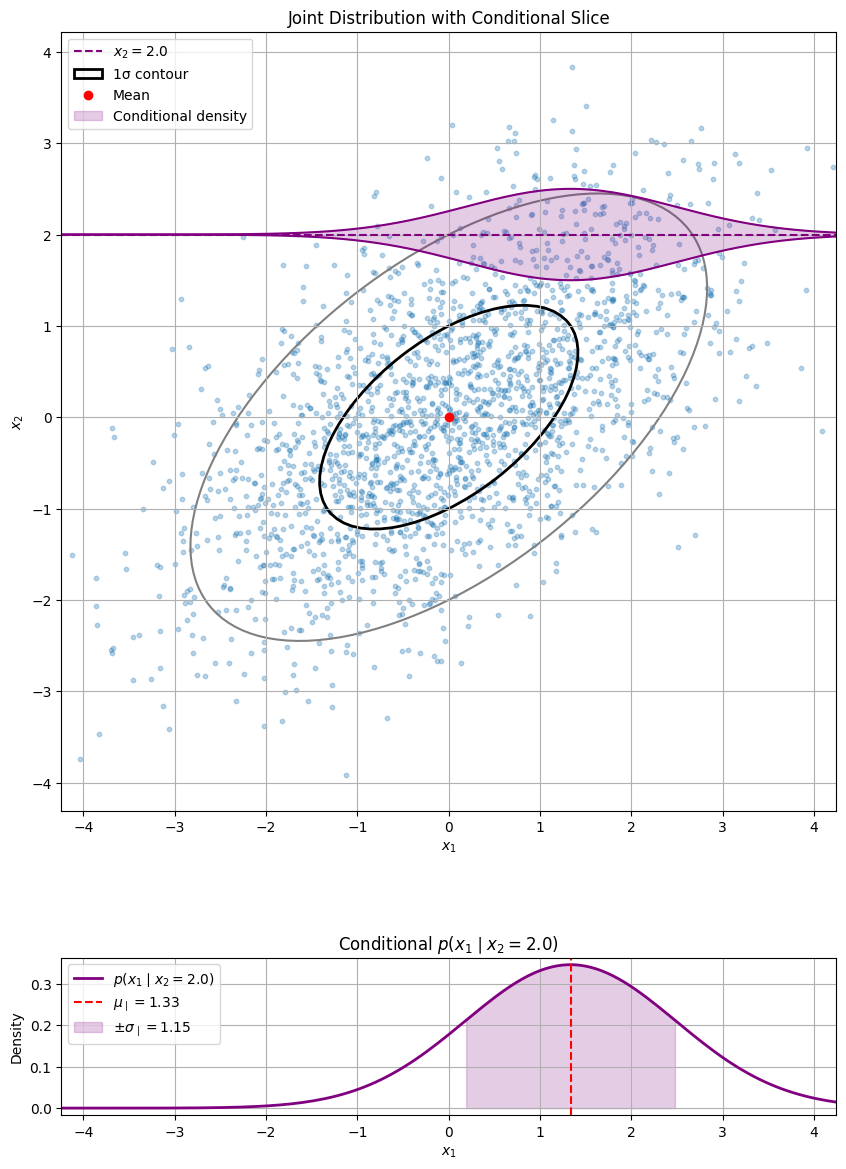
Let’s visualize a 2D example.

../_images/fa53a2783370663ab29c8b1614ba3896f450da9abc8e6fe665ce0a438c437b9b.png

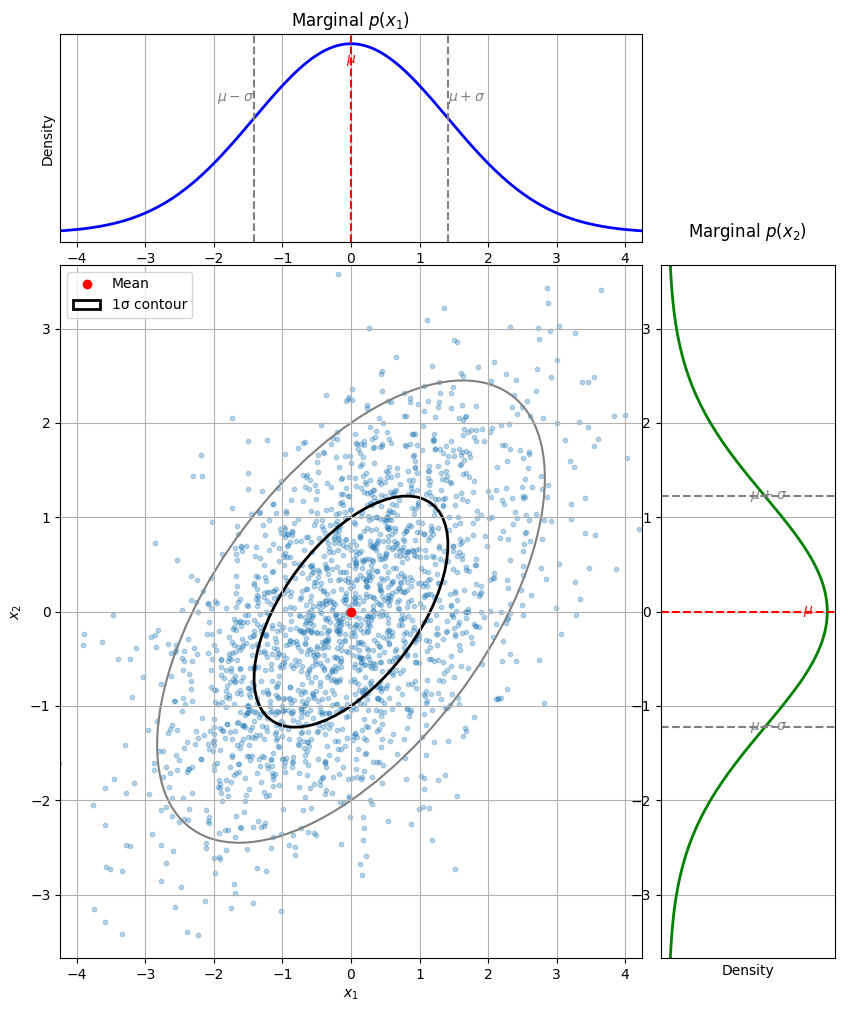
Marginal Gaussian distributions#

Let \(\mathbf{x} \sim \mathcal{N}(\boldsymbol\mu, \mathbf{\Sigma})\) be the joint distribution of two random variables \(\mathbf{x}_1\) and \(\mathbf{x}_2\), where

\[\begin{split} \mathbf{x} = \begin{bmatrix} \mathbf{x}_1 \\ \mathbf{x}_2 \end{bmatrix}, \quad \boldsymbol\mu = \begin{bmatrix} \boldsymbol\mu_1 \\ \boldsymbol\mu_2 \end{bmatrix}, \quad \mathbf{\Sigma} = \begin{bmatrix} \mathbf{\Sigma_{11}} & \mathbf{\Sigma_{12}} \\ \mathbf{\Sigma_{21}} & \mathbf{\Sigma_{22}} \end{bmatrix} \end{split}\]

The marginals of \(\mathbf{x}_1\) and \(\mathbf{x}_2\) are just Gaussians:

\[ \mathbf{x}_1 \sim \mathcal{N}(\boldsymbol\mu_1, \mathbf{\Sigma_{11}}), \quad \mathbf{x}_2 \sim \mathcal{N}(\boldsymbol\mu_2, \mathbf{\Sigma_{22}}) \]

Let’s visualize the two marginal distributions for \(\mathbf{x}_1\) and \(\mathbf{x}_2\) for the same 2-D Gaussian as above.

Show code cell source Hide code cell source

def plot_joint_with_marginals(mu, Sigma, n_samples=2000):
    samples = np.random.multivariate_normal(mu, Sigma, size=n_samples)
    x1, x2 = samples[:, 0], samples[:, 1]

    # Layout
    fig = plt.figure(figsize=(10, 12))
    gs = gridspec.GridSpec(2, 2, width_ratios=[4, 1.2], height_ratios=[1.2, 4],
                           hspace=0.05, wspace=0.05)

    ax_main = fig.add_subplot(gs[1, 0])
    ax_top = fig.add_subplot(gs[0, 0], sharex=ax_main)
    ax_right = fig.add_subplot(gs[1, 1], sharey=ax_main)

    # === Main joint plot ===
    ax_main.scatter(x1, x2, alpha=0.3, s=10)
    ax_main.plot(mu[0], mu[1], 'ro', label='Mean')
    draw_ellipse(ax_main, mu, Sigma, n_std=1, edgecolor='black', facecolor='none', lw=2, label='1σ contour')
    draw_ellipse(ax_main, mu, Sigma, n_std=2, edgecolor='gray', facecolor='none', lw=1.5)
    ax_main.set_xlabel('$x_1$')
    ax_main.set_ylabel('$x_2$')
    ax_main.set_xlim(mu[0] - 3*np.sqrt(Sigma[0,0]), mu[0] + 3*np.sqrt(Sigma[0,0]))
    ax_main.set_ylim(mu[1] - 3*np.sqrt(Sigma[1,1]), mu[1] + 3*np.sqrt(Sigma[1,1]))
    ax_main.grid(True)
    #ax_main.set_title('Joint Distribution $p(x_1, x_2)$')
    ax_main.legend()

    # === Top marginal: p(x1) ===
    std1 = np.sqrt(Sigma[0, 0])
    x1_vals = np.linspace(mu[0] - 4*std1, mu[0] + 4*std1, 200)
    y1_vals = norm.pdf(x1_vals, mu[0], std1)
    ax_top.plot(x1_vals, y1_vals, 'b-', lw=2)
    ax_top.axvline(mu[0], color='red', linestyle='--')
    ax_top.axvline(mu[0] - std1, color='gray', linestyle='--')
    ax_top.axvline(mu[0] + std1, color='gray', linestyle='--')
    ax_top.set_ylabel('Density')
    ax_top.set_yticks([])
    ax_top.grid(True)
    ax_top.set_title('Marginal $p(x_1)$')

    # Annotations for x1 marginal
    ax_top.text(mu[0], max(y1_vals)*0.9, r'$\mu$', color='red', ha='center')
    ax_top.text(mu[0] - std1, max(y1_vals)*0.7, r'$\mu - \sigma$', color='gray', ha='right')
    ax_top.text(mu[0] + std1, max(y1_vals)*0.7, r'$\mu + \sigma$', color='gray', ha='left')

    # === Right marginal: p(x2) ===
    std2 = np.sqrt(Sigma[1, 1])
    x2_vals = np.linspace(mu[1] - 4*std2, mu[1] + 4*std2, 200)
    y2_vals = norm.pdf(x2_vals, mu[1], std2)
    ax_right.plot(y2_vals, x2_vals, 'g-', lw=2)
    ax_right.axhline(mu[1], color='red', linestyle='--')
    ax_right.axhline(mu[1] - std2, color='gray', linestyle='--')
    ax_right.axhline(mu[1] + std2, color='gray', linestyle='--')
    ax_right.set_xticks([])
    ax_right.set_xlabel('Density')
    ax_right.grid(True)
    ax_right.set_title('Marginal $p(x_2)$', pad=20)

    # Annotations for x2 marginal
    ax_right.text(max(y2_vals)*0.85, mu[1], r'$\mu$', color='red', va='center')
    ax_right.text(max(y2_vals)*0.75, mu[1] - std2, r'$\mu - \sigma$', color='gray', va='center', ha='right')
    ax_right.text(max(y2_vals)*0.75, mu[1] + std2, r'$\mu + \sigma$', color='gray', va='center', ha='right')

    plt.show()
plot_joint_with_marginals(mu, Sigma, n_samples=2000)

../_images/40afa43529efaef50641d66869cd5f916894830cd85037b172d3fade72e13476.png

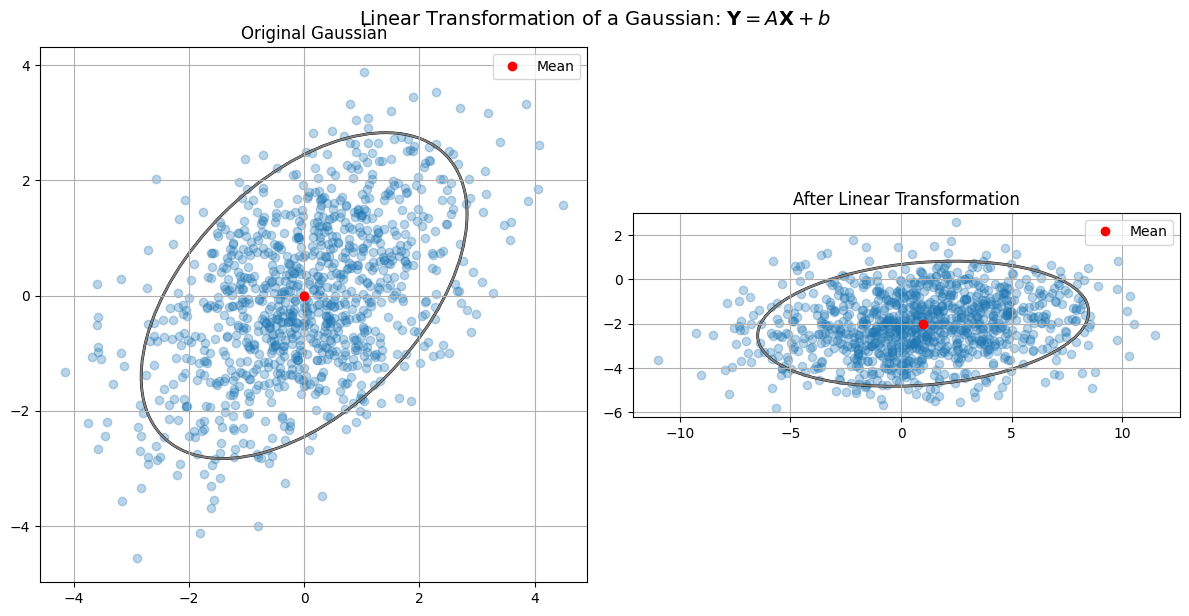
Linear Transform of a Gaussian#

Theorem (Closure of Gaussian under Affine Transformations)

Let \(\mathbf{X} \sim \mathcal{N}(\boldsymbol\mu, \mathbf{\Sigma})\)

Let \(\mathbf{Y} = \mathbf{A} \mathbf{X} + \mathbf{b}\)

Then:

\[ \mathbf{Y} \sim \mathcal{N}(\mathbf{A} \boldsymbol\mu + \mathbf{b},\ \mathbf{A} \mathbf{\Sigma} \mathbf{A}^\top) \]

Proof. (using completing the square)

Start with the Gaussian:

\[ p(\mathbf{x}) \propto \exp\left( -\frac{1}{2} (\mathbf{x} - \boldsymbol\mu)^\top \mathbf{\Sigma}^{-1} (\mathbf{x} - \boldsymbol\mu) \right) \]

Let \(\mathbf{y} = \mathbf{A} \mathbf{x} + \mathbf{b}\)

Assume \(\mathbf{A}\) is invertible: \(\mathbf{x} = \mathbf{A}^{-1}(\mathbf{y} - \mathbf{b})\)

Then:

\[ p_{\mathbf{Y}}(\mathbf{y}) \propto \exp\left( -\frac{1}{2} \left( \mathbf{A}^{-1}(\mathbf{y} - \mathbf{b}) - \boldsymbol\mu \right)^\top \mathbf{\Sigma}^{-1} \left( \mathbf{A}^{-1}(\mathbf{y} - \mathbf{b}) - \boldsymbol\mu \right) \right) \]

Let’s define:

\[ \boldsymbol\mu_Y = \mathbf{A} \boldsymbol\mu + \mathbf{b} \quad \text{and} \quad \mathbf{\Sigma}_Y = \mathbf{A} \mathbf{\Sigma} \mathbf{A}^\top \]

As shown earlier by completing the square, this is again of the form:

\[ p(\mathbf{y}) \propto \exp\left( -\frac{1}{2} (\mathbf{y} - \boldsymbol\mu_Y)^\top \mathbf{\Sigma}_Y^{-1} (\mathbf{y} - \boldsymbol\mu_Y) \right) \]

Thus, \(\mathbf{Y} \sim \mathcal{N}(\boldsymbol\mu\_Y, \mathbf{\Sigma}\_Y)\).

While we have shown this for the case of an invertible \(\mathbf{A}\), the result holds for any \(\mathbf{A}\). The proof is more involved in this case, but the result is the same.

Let’s visualize this with a simple 2D Gaussian and its linear transformation.

../_images/44a30d7b00025ffbe7764e010c37f5f4048b8bd836beb85ef8b603d72c1fe56e.png

Example: Linear Regression estimates under Gaussian noise are Gaussian#

Let’s consider the linear regression model:

\[ y_i = \mathbf{x}_i^\top \boldsymbol\beta + \epsilon_i \]

where \(\epsilon_i \sim \mathcal{N}(0, \sigma^2)\) is i.i.d. Gaussian noise.

Let’s assume that we have a training set \(\mathcal{D}=\{(\mathbf{x}_i, y_i)\}_{i=1}^n\) and we want to estimate the parameters \(\boldsymbol\beta\).

We can write this as

\[ \mathbf{y} = \mathbf{X}\boldsymbol\beta + \boldsymbol\epsilon \]

where \(\mathbf{X}\in\mathbb{R}^{n\times d}\) is the design matrix, \(\boldsymbol\beta\in\mathbb{R}^d\) is the parameter vector, and \(\boldsymbol\epsilon\in\mathbb{R}^n\) is the noise vector.

1. The vector of all training samples \(\mathbf{y}\in\mathbb{R}^n\) follows a Gaussian distribution.#

We observe, that in the model, the vector of all training samples \(\mathbf{y}\in\mathbb{R}^n\) follows a Gaussian distribution.

\[ \mathbf{y} \sim \mathcal{N}(\mathbf{X}\boldsymbol\beta, \sigma^2\mathbf{I}) \]

where \(\boldsymbol\epsilon \sim \mathcal{N}(\mathbf{0}, \sigma^2\mathbf{I})\).

The mean of \(\mathbf{y}\) is \(\mathbf{X}\boldsymbol\beta\) and the variance is \(\sigma^2\mathbf{I}\).

2. The OLS and Ridge estimates are Gaussian.#

Say, we use either the OLS \((\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top\mathbf{y}\) or the Ridge estimator \((\mathbf{X}^\top\mathbf{X}+\lambda\mathbf{I})^{-1}\mathbf{X}^\top\mathbf{y}\) to estimate \({\boldsymbol\beta}\).

Then, as these are affine transformations of the Gaussian \(\mathbf{y}\), the estimates are also Gaussian.

\[ \hat{\boldsymbol\beta}_{OLS} \sim \mathcal{N}(\boldsymbol\beta, \sigma^2(\mathbf{X}^\top\mathbf{X})^{-1}) \]

\[ \hat{\boldsymbol\beta}_{Ridge} \sim \mathcal{N}(\boldsymbol\beta, \sigma^2(\mathbf{X}^\top\mathbf{X}+\lambda\mathbf{I})^{-1}) \]

This result is typically used in statistics to compute confidence intervals for the estimates or to test hypotheses about the parameters.

3. The predictions are Gaussian.#

The predictions are also Gaussian.

\[ \mathbf{y}_{new} \sim \mathcal{N}(\mathbf{X}_{new}\hat{\boldsymbol\beta}, \sigma^2) \]

where \(\mathbf{X}_{new}\in\mathbb{R}^{n_{new}\times d}\) is the design matrix for the new samples and \(\hat{\boldsymbol\beta}\) is the estimated parameter vector, which is Gaussian as shown in 2.

Thus, the predictions are also Gaussian, reflecting the uncertainty in the predictions.

The following example visualizes this property.

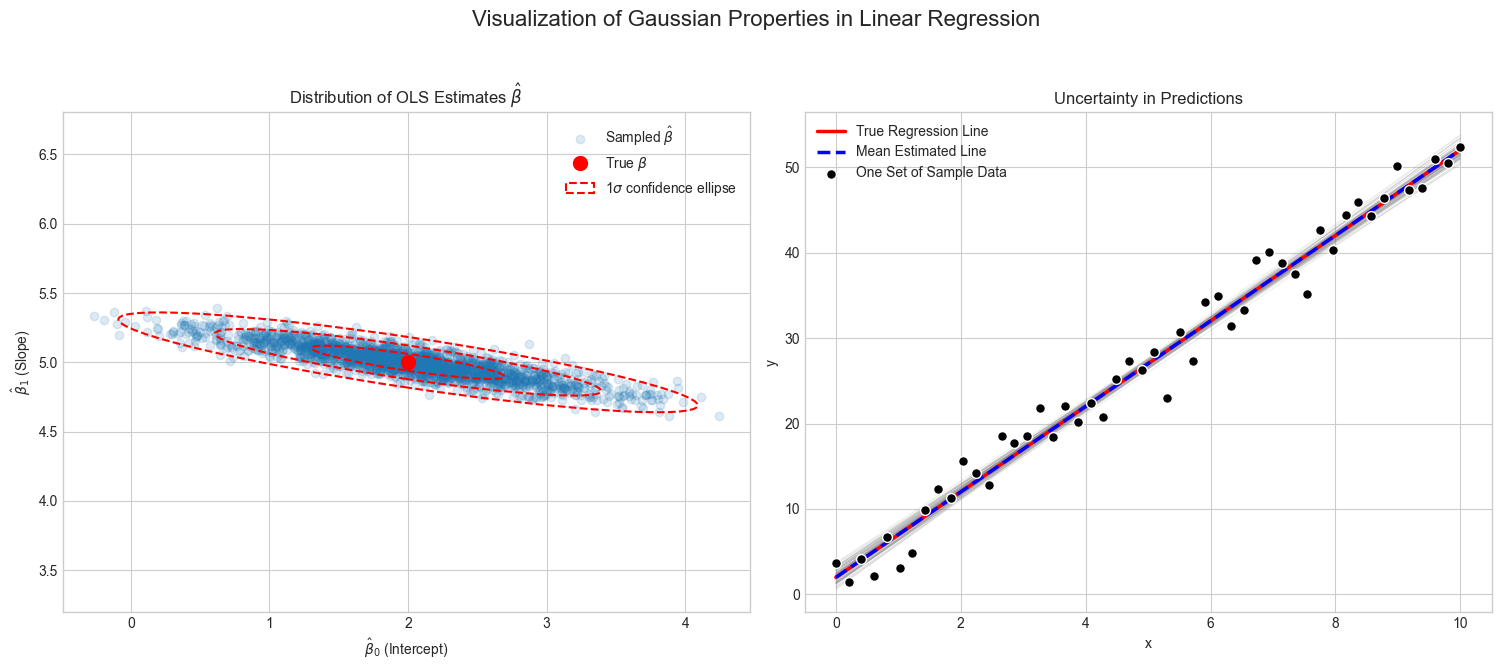
We repeatedly generate data from a true linear model with added Gaussian noise, and for each dataset, it computes the OLS estimate \(\hat{\boldsymbol\beta}\).

The visualization shows two things:

A scatter plot of all the estimated parameter pairs \((\hat{\beta}0, \hat{\beta}_1)\), which form a Gaussian cloud around the true parameter value, as predicted by the theory.
A plot showing multiple regression lines, each corresponding to a different \(\hat{\boldsymbol\beta}\) estimate. This illustrates how the uncertainty in the parameters translates directly into uncertainty about the model’s predictions.