Extreme Value Theorem#
The Extreme Value Theorem states that if a function is continuous on a closed interval, then it attains both a maximum and a minimum value on that interval. This theorem is crucial in optimization problems, as it guarantees the existence of optimal solutions within bounded domains.
Theorem (Extreme Value Theorem)
If a function \(f:[a,b] \to \mathbb{R}\) is continuous on a closed and bounded interval \([a,b]\), then \(f\) attains both a minimum and a maximum value on this interval. That is, there exist points \(x_{\min}, x_{\max} \in [a,b]\) such that:
The Extreme Value Theorem states that any continuous function defined on a closed, bounded interval must attain both a maximum and a minimum value at least once within that interval. This theorem leverages continuity and the compactness of the interval, ensuring no infinite “jumps” or “holes” exist in the graph.
The following visualization demonstrates the EVT on a continuous function on a closed interval, explicitly marking the points at which the function achieves its maximum and minimum values.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
# Define a continuous function
def f(x):
return np.sin(x) + 0.2 * x
# Define the closed interval [a, b]
a, b = 0, 4 * np.pi
x = np.linspace(a, b, 1000)
y = f(x)
# Find maximum and minimum points numerically
x_max = x[np.argmax(y)]
y_max = np.max(y)
x_min = x[np.argmin(y)]
y_min = np.min(y)
# Plotting the function
plt.figure(figsize=(10, 6))
plt.plot(x, y, label=r'$f(x)=\sin(x)+0.2x$', color='blue')
plt.scatter([x_max, x_min], [y_max, y_min], color='red', zorder=5)
plt.annotate('Maximum', (x_max, y_max), xytext=(x_max, y_max+0.5),
arrowprops=dict(arrowstyle='->', lw=1.5))
plt.annotate('Minimum', (x_min, y_min), xytext=(x_min, y_min-0.5),
arrowprops=dict(arrowstyle='->', lw=1.5))
plt.title('Visualization of Extreme Value Theorem')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid(True)
plt.legend()
plt.show()
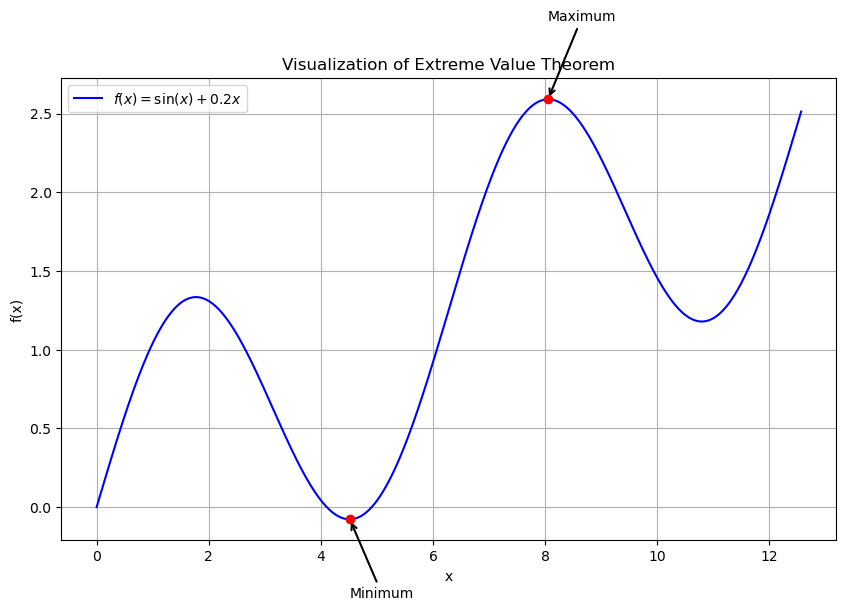
We see that within the interval \([a,b]\), the continuous function \(f(x)\) attains both its absolute maximum and absolute minimum at distinct points. The red points highlight the exact locations of these extreme values, illustrating clearly the conclusion of the Extreme Value Theorem.
Proof. Extreme Value Theorem.
The proof relies on two important properties: continuity and compactness (closedness and boundedness) of the interval.
Step 1: Compactness of the interval
Consider the interval \([a,b]\subset\mathbb{R}\).
It is bounded, because \(a\) and \(b\) are finite.
It is closed, because it contains its endpoints.
Thus, the interval \([a,b]\) is compact (closed and bounded).
Step 2: Boundedness of the continuous function on a compact interval
Assume for contradiction that the continuous function \(f\) is not bounded above.
Then, for every integer \(n\), there exists some \(x_n \in [a,b]\) with \(f(x_n) > n\). This defines a sequence \((x_n)\subseteq[a,b]\).
Since \([a,b]\) is compact, by the Bolzano–Weierstrass theorem, the sequence \((x_n)\) has a convergent subsequence \((x_{n_k})\) converging to some limit \(x^*\in[a,b]\).
By continuity of \(f\):
But we know \(f(x_{n_k})\to\infty\) as \(k\to\infty\), contradicting the fact that the limit must be finite. Hence, \(f\) must be bounded above.
The argument for boundedness below is similar: if \(f\) were unbounded below, we would similarly reach a contradiction. Thus, \(f\) is bounded both above and below.
Step 3: Existence of maximum and minimum
Let’s first prove existence of a maximum value (the proof for minimum is symmetric):
Define the supremum of the set \(f([a,b])\):
Since \(f\) is bounded above, \(M\) is finite.
To show \(f\) attains the value \(M\), assume for contradiction that it does not. Then, for all \(x\in[a,b],\) we have \(f(x)<M.\) Define the function \(g(x)=\frac{1}{M - f(x)}\). Clearly, \(g\) is continuous on \([a,b]\) (because the denominator is never zero by our assumption).
Since \([a,b]\) is compact and \(g\) is continuous, \(g\) must be bounded. However, as \(f(x)\) approaches \(M\), the denominator \(M - f(x)\) approaches zero, making \(g(x)\) grow without bound. Thus, there must exist a sequence \(x_n\) in \([a,b]\) such that \(f(x_n)\to M\).
Again, by compactness (Bolzano–Weierstrass theorem), there exists a subsequence \(x_{n_k}\to x^*\in[a,b]\). By continuity of \(f\), we have:
This shows that the function indeed attains its maximum at some point \(x^*\in[a,b]\).
By symmetry, \(f\) also attains its minimum in a similar manner.