Rolle’s theorem#
Rolle’s theorem states that if a function is continuous on a closed interval and differentiable on the open interval, and if the function takes the same value at both endpoints, then there exists at least one point in the open interval where the derivative is zero.
Theorem (Rolles theorem)
Let \(f:[a,b]\rightarrow\mathbb{R}\) be a function satisfying the following three conditions:
\(f\) is continuous on the closed interval \([a,b]\).
\(f\) is differentiable on the open interval \((a,b)\).
\(f(a)=f(b)\).
Then, there exists some \(c\in(a,b)\) such that:
In other words, there’s at least one point where the tangent to the graph of \(f(x)\) is horizontal.
We visually demonstrate Rolle’s theorem by plotting a function meeting the theorem’s conditions and highlighting a point where the tangent line is horizontal:
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
# Define a continuous and differentiable function with f(a)=f(b)
def f(x):
return (x - 2) * (x - 4) * (x - 6)
# Derivative of the function
def f_prime(x):
return 3*x**2 - 24*x + 44
# Interval endpoints
a, b = 2, 6
x_vals = np.linspace(a, b, 500)
y_vals = f(x_vals)
# Find critical points numerically (where f'(x)=0)
critical_guess = [3, 5] # Initial guesses close to expected roots
critical_points = fsolve(f_prime, critical_guess)
critical_points = [c for c in critical_points if a < c < b]
# Plot the function
plt.figure(figsize=(10, 6))
plt.plot(x_vals, y_vals, label='$f(x)$', color='blue')
# Highlight endpoints
plt.scatter([a, b], [f(a), f(b)], color='black', zorder=5)
plt.text(a, f(a), ' $a$', fontsize=12, verticalalignment='bottom')
plt.text(b, f(b), '$b$ ', fontsize=12, verticalalignment='bottom', horizontalalignment='right')
# Highlight critical points (horizontal tangent)
for c in critical_points:
plt.scatter(c, f(c), color='red', zorder=5)
plt.plot([c-0.5, c+0.5], [f(c), f(c)], '--', color='red', label='Horizontal tangent' if c == critical_points[0] else '')
plt.title("Visualization of Rolle's Theorem")
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.axhline(0, color='black', lw=0.5)
plt.grid(True)
plt.legend()
plt.show()
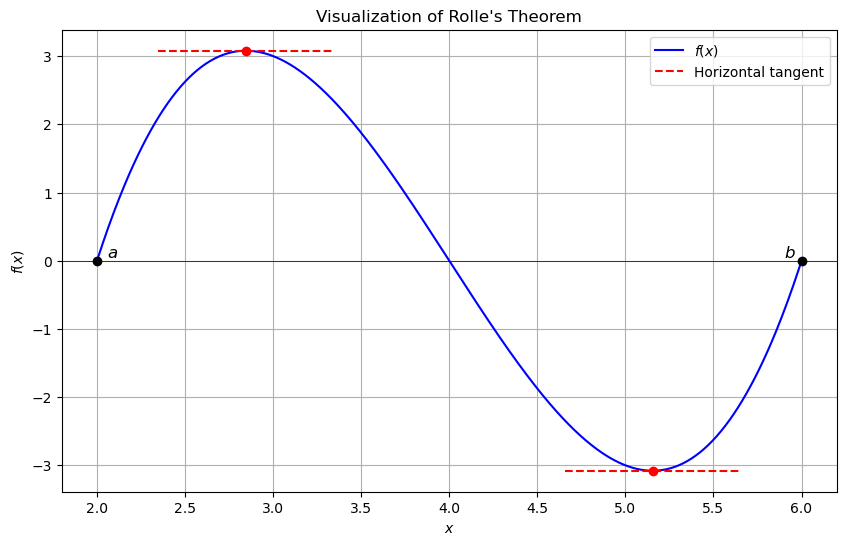
The visualized function is continuous and differentiable, and the endpoints have equal function values, \(f(a)=f(b)\). The red points and dashed horizontal lines represent critical points where the derivative is zero—demonstrating the theorem’s guarantee that at least one horizontal tangent line exists within the interval.
Proof. Rolle’s theorem.
Step 1 (special case): If \(f(x)\) is constant, say \(f(x)=k\), then clearly \(f'(x)=0\) everywhere on \((a,b)\). Hence, Rolle’s theorem trivially holds.
Step 2 (general case): Suppose \(f(x)\) is not constant on \([a,b] \). Since \(f(x)\) is continuous on the compact interval \([a,b]\), by the Extreme Value Theorem, it must attain a maximum and minimum on this interval. Let’s denote by \(x_{\max}\in[a,b]\) the point at which \(f\) attains its maximum.
Step 3 (Maximum inside interval): There are two possibilities:
If \(x_{\max}\) lies in the open interval \((a,b) \), then since \(f(x_{\max})\) is a maximum, the derivative at this point, provided it exists, must be zero. Thus, setting \(c=x_{\max}\), we have \(f'(c)=0\), completing the proof.
If \(x_{\max}\) lies at one of the endpoints, say \(x_{\max}=a\), then since \(f(a)=f(b)\), the maximum at \(a\) implies the function must be less or equal to \(f(a)\) throughout \((a,b)\). Because \(f\) is continuous and differentiable on \((a,b)\), we consider the following scenarios:
If \(f(x)<f(a)\) for all \(x\in(a,b)\), then \(f\) strictly decreases immediately after \(a\), implying \(f'(a)<0\), contradicting differentiability at endpoint (since differentiability is only assumed on \((a,b)\), we actually do not consider the derivative exactly at endpoint here; however, differentiability inside the interval implies the function is smoothly transitioning away from endpoints). Still, even without directly using endpoint derivatives, the fact remains that there must exist another critical point inside the interval due to continuity and differentiability constraints, or otherwise the function would monotonically decrease, contradicting the equality \(f(a)=f(b)\). Thus, the maximum cannot be exclusively at an endpoint without another interior maximum or minimum. Hence, there must exist at least one critical point with zero derivative within the interval.
Step 4 (Conclusion): In every possible scenario, there must exist a point \(c\in(a,b)\) such that \(f'(c)=0\).