Gaussian-Process Latent Variable Model (GPLVM) with Input Optimisation

Gaussian-Process Latent Variable Model (GPLVM) with Input Optimisation#

🌟 Motivation#

Real-world data often lies on complex, curved surfaces or manifolds in a high-dimensional space. Think of images, speech signals, or biological measurements: although high-dimensional, they typically possess a much simpler underlying structure. Can we automatically discover such a simplified, low-dimensional structure from complex data?

A powerful solution to this question is the Gaussian-Process Latent Variable Model (GPLVM):

  • GPLVM elegantly extends Gaussian Processes to unsupervised learning, automatically discovering low-dimensional representations.

  • It reveals the intrinsic structure hidden in high-dimensional observations by optimising latent input positions.

  • It outperforms linear methods (like PCA) in capturing nonlinear relationships and structure.

In short: GPLVM helps you “unroll” complex manifolds, simplifying data representation and interpretation.

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_swiss_roll
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE

# Generate smaller Swiss roll dataset for fast visualization
n_samples = 500
X, color = make_swiss_roll(n_samples, noise=0.05)
X = X[:, [0, 2, 1]]  # reorder axes for better visualization

# Apply PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

# Faster t-SNE with fewer iterations and lower perplexity
tsne = TSNE(n_components=2, init='pca', random_state=42, perplexity=20, n_iter=500)
X_tsne = tsne.fit_transform(X)

# Plot
fig = plt.figure(figsize=(15, 4))

# 3D Swiss Roll
ax = fig.add_subplot(131, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral, s=10)
ax.set_title("Original 3D Swiss Roll")
ax.view_init(10, -70)

# PCA
plt.subplot(132)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=color, cmap=plt.cm.Spectral, s=10)
plt.title("PCA Projection")
plt.xlabel("PC 1")
plt.ylabel("PC 2")

# t-SNE (motivates GPLVM)
plt.subplot(133)
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=color, cmap=plt.cm.Spectral, s=10)
plt.title("t-SNE Embedding (Nonlinear)")
plt.xlabel("Dim 1")
plt.ylabel("Dim 2")

plt.suptitle("Motivation for GPLVM: Recovering Low-Dimensional Manifolds", fontsize=14)
plt.tight_layout()
plt.subplots_adjust(top=0.85)
plt.show()

/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/manifold/_t_sne.py:1164: FutureWarning: 'n_iter' was renamed to 'max_iter' in version 1.5 and will be removed in 1.7.
  warnings.warn(
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/utils/extmath.py:335: RuntimeWarning: divide by zero encountered in matmul
  Q, _ = normalizer(A @ Q)
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/utils/extmath.py:335: RuntimeWarning: overflow encountered in matmul
  Q, _ = normalizer(A @ Q)
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/utils/extmath.py:335: RuntimeWarning: invalid value encountered in matmul
  Q, _ = normalizer(A @ Q)
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/utils/extmath.py:336: RuntimeWarning: divide by zero encountered in matmul
  Q, _ = normalizer(A.T @ Q)
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/utils/extmath.py:336: RuntimeWarning: overflow encountered in matmul
  Q, _ = normalizer(A.T @ Q)
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/utils/extmath.py:336: RuntimeWarning: invalid value encountered in matmul
  Q, _ = normalizer(A.T @ Q)
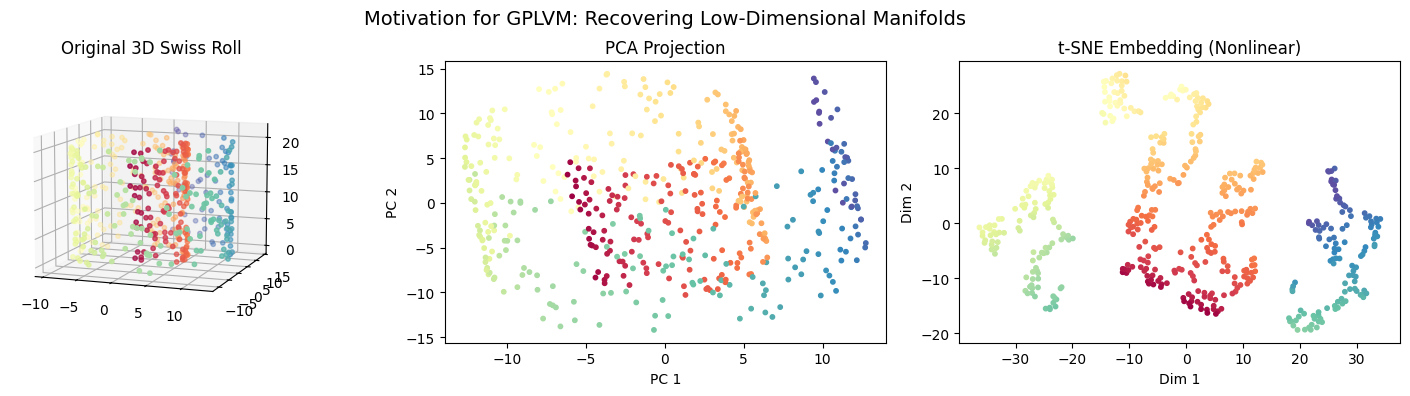
../_images/c675339f89bc79c60df9f53613eba946edcce8efb36bad72f141fd20543ace34.png

This visualization shows:

  • Left: the true high-dimensional manifold structure.

  • Middle: PCA, a linear method that fails to “unroll” the manifold.

  • Right: t-SNE, a nonlinear method that recovers the latent 2D structure (like GPLVM aims to do, but with a probabilistic model).

📌 What You Will Do in This Project#

Your main goal is straightforward yet powerful:

Implement a Gaussian-Process Latent Variable Model (GPLVM) to find a meaningful 2-D latent representation of the classic 3-D Swiss-roll dataset.

You will:

  • Implement GPLVM from scratch, using NumPy.

  • Optimise latent variables (input points in latent space) and kernel hyperparameters simultaneously.

  • Visualise your learned latent embedding clearly to show how GPLVM uncovers the underlying 2-D structure hidden in the data.

🔍 Key Concepts You’ll Master#

Through this project, you’ll build practical skills around these key ideas:

  • Latent Variable Modelling: Understanding how latent inputs (unobserved) can be optimised to explain complex observed data effectively.

  • GP Marginal Likelihood and MAP: You’ll learn how the marginal likelihood of Gaussian Processes guides simultaneous optimisation of latent variables and kernel hyperparameters.

  • Alternating Optimisation: Discover how to iteratively optimise latent inputs and kernel parameters to reveal meaningful low-dimensional representations.

  • Nonlinear Dimensionality Reduction: Compare how GPLVM performs better than linear methods (PCA), providing more interpretable embeddings.

🚧 Core Tasks (Implementation Details)#

You will practically engage with these tasks:

  • Latent Initialisation (PCA): Begin by initialising latent 2-D positions for your data points using PCA, providing a sensible starting point.

  • Alternating Optimisation: Perform iterative optimisation steps, alternating between:

    • Optimising latent inputs (X).

    • Optimising kernel hyperparameters (length-scale, signal variance, noise variance).

  • Visualization: Create clear visualisations of your latent embedding (2-D space) colour-coded by the height of the original Swiss-roll, showing clearly how GPLVM effectively “unrolls” the manifold.

📝 Reporting: Analysis and Insights#

Your short report (~2 pages) should focus on insightful comparisons and explanations:

  • Show derivation of the GPLVM.

  • Clearly explain why GPLVM provides a more meaningful embedding than PCA for nonlinear data like the Swiss-roll.

  • Visually illustrate your embedding, highlighting key structural features and smoothness of the learned representation.

  • Briefly discuss how optimising both inputs and kernel parameters leads to more powerful dimensionality reduction.

🚀 Stretch Goals (Optional, Advanced)#

If you’re keen to explore further, you might:

  • Implement back-constraints: add parametric mappings to better generalise to new data points.

  • Compare GPLVM embedding to other nonlinear methods such as t-SNE, highlighting differences in interpretability and manifold preservation.

📚 Resources and Support#

  • Starter code for data generation (Swiss-roll) and visualisation will be provided, enabling you to focus on the core GPLVM implementation.

  • Feel free to leverage external resources, lecture notes, and clearly documented AI-assistance.

✅ Why This Matters#

GPLVM is not just a fascinating theoretical concept; it’s highly practical and valuable in real-world contexts:

  • Widely used in fields such as bioinformatics, robotics, computer vision, and data visualization.

  • Provides deep intuition into nonlinear dimensionality reduction, latent-variable modeling, and Gaussian processes—crucial topics in modern machine learning.

  • Demonstrates your ability to implement complex probabilistic models, optimally position latent variables, and interpret sophisticated models visually and mathematically.

This project is an opportunity to create a standout portfolio piece and gain robust understanding and confidence in modern nonlinear probabilistic modeling.

Project Summary: Gaussian-Process Latent Variable Model (GPLVM) with Input Optimization#

(NumPy)

Item

Details

Goal

Fit a 2-D latent representation for 3-D Swiss-roll using GPLVM MAP.

Key ideas

Latent \(X\) as parameters, GP marginal likelihood, alternating optimisation.

Core tasks

  • Initialise latent \(X\) with PCA.
  • Alternate optimise \(X\) and kernel hyper-parameters (few steps).
  • Visualise latent 2-D embedding colour-coded by height.

Report

Show derivation of the GPLVM; explain why GPLVM can “unroll” the manifold better than PCA.

Stretch

Add back-constraints or compare to t-SNE.
Contents