Gaussian Processes with Kernel Optimization

Gaussian Processes with Kernel Optimization#

🌟 Motivation#

When dealing with regression problems, you’ve often fitted simple linear models. But real-world data can be much more complex, nonlinear, and uncertain. How can we model such complexities accurately, while also quantifying our uncertainty about predictions?

Gaussian Processes (GP) offer a powerful Bayesian approach for regression that directly addresses these questions:

  • They elegantly combine flexibility and simplicity, offering a fully probabilistic framework.

  • GPs naturally quantify uncertainty, clearly indicating how confident we are in our predictions.

  • Kernel functions give us a powerful way to control the smoothness and complexity of our model, adapting automatically to data.

This project will give you practical experience building a GP regression model from scratch, using NumPy, and show how to optimize hyperparameters to fit data robustly.

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel, ConstantKernel as C

# Generate synthetic 1D data
def f(x):
    return np.sin(2 * np.pi * x)

rng = np.random.RandomState(42)
X_plot = np.linspace(0, 1, 500).reshape(-1, 1)
X_full = np.sort(rng.rand(30)).reshape(-1, 1)
y_full = f(X_full).ravel() + rng.normal(0, 0.1, X_full.shape[0])

# Visualize for different training sizes
training_sizes = [5, 10, 30]
fig, axes = plt.subplots(1, len(training_sizes), figsize=(18, 4), sharey=True)

for i, n in enumerate(training_sizes):
    X = X_full[:n]
    y = y_full[:n]

    # GP with RBF kernel + noise
    kernel = C(1.0, (1e-3, 1e3)) * RBF(length_scale=0.3, length_scale_bounds=(1e-2, 1e1)) + WhiteKernel(noise_level=0.1, noise_level_bounds=(1e-5, 1e0))
    gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10, random_state=0)
    gp.fit(X, y)
    
    y_pred, y_std = gp.predict(X_plot, return_std=True)

    ax = axes[i]
    ax.plot(X_plot, f(X_plot), 'k--', label="True function")
    ax.scatter(X, y, c='black', s=30, label="Training points")
    ax.plot(X_plot, y_pred, 'b-', label="GP mean")
    ax.fill_between(X_plot.ravel(), y_pred - 2*y_std, y_pred + 2*y_std, color='blue', alpha=0.2, label="±2σ band")
    ax.set_title(f"n = {n} samples")
    ax.set_ylim(-2, 2)
    ax.grid(True)

axes[0].set_ylabel("y")
for ax in axes:
    ax.set_xlabel("x")

axes[0].legend(loc="upper right")
fig.suptitle("Gaussian Process Regression: Posterior Mean and Uncertainty", fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()

/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/gaussian_process/_gpr.py:441: RuntimeWarning: divide by zero encountered in matmul
  y_mean = K_trans @ self.alpha_
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/gaussian_process/_gpr.py:441: RuntimeWarning: overflow encountered in matmul
  y_mean = K_trans @ self.alpha_
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/gaussian_process/_gpr.py:441: RuntimeWarning: invalid value encountered in matmul
  y_mean = K_trans @ self.alpha_
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/gaussian_process/_gpr.py:441: RuntimeWarning: divide by zero encountered in matmul
  y_mean = K_trans @ self.alpha_
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/gaussian_process/_gpr.py:441: RuntimeWarning: overflow encountered in matmul
  y_mean = K_trans @ self.alpha_
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/gaussian_process/_gpr.py:441: RuntimeWarning: invalid value encountered in matmul
  y_mean = K_trans @ self.alpha_
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/gaussian_process/_gpr.py:441: RuntimeWarning: divide by zero encountered in matmul
  y_mean = K_trans @ self.alpha_
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/gaussian_process/_gpr.py:441: RuntimeWarning: overflow encountered in matmul
  y_mean = K_trans @ self.alpha_
/Users/christoph/miniconda3/lib/python3.13/site-packages/sklearn/gaussian_process/_gpr.py:441: RuntimeWarning: invalid value encountered in matmul
  y_mean = K_trans @ self.alpha_
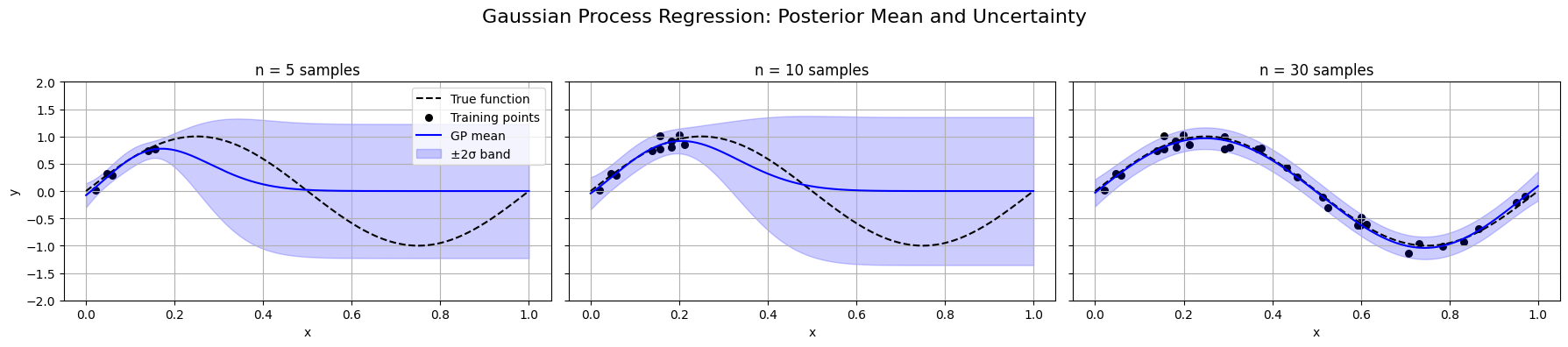
../_images/dc3f55cbadf81d17d1605617275efd22b3e70fb3b42f41e0825f8ae9f5bb815a.png

Here is a figure visualizing key concepts of Gaussian Processes with Kernel Optimization:

  • The GP posterior mean (blue line) adapts to increasing training data (n = 5, 10, 30).

  • The shaded ±2σ confidence band shows predictive uncertainty—narrowing as data increases.

  • The model automatically adjusts its fit through kernel hyperparameter optimization using marginal likelihood.

📌 What You Will Do in This Project#

Your clear, achievable goal is:

Implement a 1-D Gaussian Process regression model with an RBF kernel, optimizing hyperparameters via marginal likelihood maximization.

In this hands-on project, you’ll:

  • Code from scratch the GP predictive mean and variance calculations using a Radial Basis Function (RBF) kernel.

  • Implement a numerical optimization procedure (L-BFGS or simple grid search) to optimize hyperparameters:

    • length-scale \(\ell\),

    • signal variance \(\sigma_f^2\),

    • noise variance \(\sigma_n^2\).

  • Clearly visualize your fitted GP model predictions with ±2σ uncertainty bands for increasing numbers of training samples (n = 5, 10, 30).

🔍 Key Concepts You’ll Master#

Through this project, you’ll gain practical mastery of several important concepts:

  • Gaussian Processes fundamentals: How GP regression works as a Bayesian method, providing predictive distributions, not just single predictions.

  • Kernel hyperparameter optimization: Learn how to objectively tune your kernel parameters (\(\ell,\sigma_f,\sigma_n\)) by maximizing the marginal likelihood (evidence).

  • Numerical Stability and Efficiency: Implement the Cholesky decomposition method for stable and efficient GP inference and optimization.

  • Uncertainty quantification: Clearly visualize prediction uncertainty and understand its importance in real-world decision-making.

🚧 Core Tasks (Implementation Details)#

You’ll proceed with these practical steps:

  • RBF kernel implementation: Code up a clean and efficient RBF kernel in NumPy.

  • GP predictive equations: Compute the GP posterior mean and variance predictions from training data, clearly handling numerical stability (Cholesky solves and log-determinants).

  • Hyperparameter optimization: Use an optimizer (scipy.optimize or grid search) to find the best kernel hyperparameters by maximizing the marginal likelihood (evidence).

  • Visualization of Uncertainty: Clearly plot your GP predictions with ±2σ confidence intervals for different amounts of training data (n = 5, 10, 30) to see how uncertainty evolves as more data is added.

📝 Reporting: Analysis and Insights#

Your concise report (~2 pages) should focus on clear insights, specifically:

  • Derivation of the GP: Derive the GP as kernelized Bayesian linear regression.

  • Plot how the marginal likelihood (evidence) surface changes with different values of length-scale (\(\ell\)).

  • Discuss over-fitting and under-fitting: What happens when your length-scale is too small or too large?

  • Clearly visualize how increasing data (n=5→30) reduces uncertainty and improves predictions.

🚀 Stretch Goals (Optional, Advanced)#

If you’re keen to deepen your understanding, consider:

  • Exploring more complex kernels (Matérn, periodic, etc.) and comparing their performance.

  • Implementing automatic differentiation with scipy.optimize or other frameworks to efficiently optimize hyperparameters.

📚 Resources and Support#

  • You’ll receive a starter notebook with synthetic datasets to streamline the implementation and visualization process.

  • Feel free to use external resources, lecture materials, and AI-assisted coding (clearly documented).

✅ Why This Matters#

Gaussian Processes are widely used in industry and research due to their powerful predictive capabilities and robust uncertainty quantification:

  • They are central in fields like geostatistics, finance, hyperparameter tuning, and Bayesian optimization.

  • Understanding GP regression deeply enhances your practical skills in probabilistic modeling and optimization—essential competencies in modern machine learning.

This project will equip you with hands-on experience, enabling you to confidently apply GPs to real-world tasks and present an insightful portfolio piece.

Project Summary: Gaussian Processes with Kernel Optimization#

(NumPy)

Item

Details

Goal

Build 1-D GP regression with RBF kernel; learn length-scale via marginal log-likelihood maximisation (L-BFGS or grid).

Key ideas

Cholesky solves, log-det, automatic differentiation optional (scipy.optimize).

Core tasks

  • Implement predictive mean/variance.
  • Optimise \(\ell,\sigma_f,\sigma_n\).
  • Plot posterior mean ±2σ bands for n = {5,10,30} samples.

Report

Show derivation of the GP; show how evidence surface changes with \(\ell\); comment on over/under-fitting.

Stretch

Explore more complex kernels (Matérn, periodic, etc.); implement automatic differentiation.
Contents